MATEMATIKA-STATISTIKA-PERTEMUAN 3

 

Statistika adalah cabang dari matematika yang mempelajari cara mengumpulkan data, menyusun data, menyajikan data, mengolah dan menganalisis data, menarik kesimpulan, dan menafsirkan parameter.

Kegiatan Statistika meliputi:

1. Mengumpulkan data

2. Menyusun data

3. Menyajikan data

4. Mengolah dan Menganalisis data 

5. Menarik kesimpulan

6. Menafsirkan

1. Pengertian Datum dan Data

Data adalah catatan atas kumpulan fakta.  Dalam penggunaan sehari-hari data berarti suatu pernyataan yang diterima secara apa adanya. Pernyataan ini adalah hasil pengukuran atau pengamatan suatu variabel yang bentuknya dapat berupa angka, kata-kata, atau citra. 

Macam-macam Jenis Data

Berdasarkan jenisnya, data dibedakan menjadi 2 macam, yaitu:

1. Data Kuantitatif, yaitu data yang berupa bilangan dan nilainya bisa berubah-ubah. Contoh: Jumlah siswa Kelas XI SMA N 1 Kluet Timur sebanyak 200 siswa.
2. Data Kualitatif, yaitu data yang menggambarkan keadaan objek yang dimaksud. Contoh : Selain ramah, Andri juga pintar

Pengertian datum adalah informasi atau keterangan yang diperoleh dari suatu pengamatan yang berupa angka, simbol atau bahasa (sifat). 

    

2. Pengertian Populasi dan Sampel 

Misal, seorang peneliti ingin meneliti tinggi badan rata-rata siswa SMA di Kabupaten Asel. Kemudian, ia kumpulkan data tentang tinggi badan seluruh siswa SMA di Kabupaten Asel. Data tinggi badan seluruh siswa SMA di Kabupaten Asel disebut populasi. Namun, karena ada beberapa kendala seperti keterbatasan waktu, dan biaya, maka data tinggi badan seluruh siswa SMA di Kabupaten Asel akan sulit diperoleh. Untuk mengatasinya, dilakukan pengambilan tinggi badan dari beberapa siswa SMA di Kabupaten Asel yang dapat mewakili keseluruhan siswa SMA di Kabupaten Asel. Data tersebut dinamakan data dengan nilai perkiraan, sedangkan sebagian siswa SMA yang dijadikan objek penelitian disebut sampel. Agar diperoleh hasil yang berlaku secara umum maka dalam pengambilan sampel, diusahakan agar sampel dapat mewakili populasi.

3. Pengumpulan Data

Menurut sifatnya, data dibagi menjadi 2 golongan, yaitu

sebagai berikut.

1)  Data kuantitatif adalah data yang berbentuk angka atau

     bilangan. Data kuantitatif terbagi atas dua bagian, yaitu

     data cacahan dan data ukuran.

     a) Data cacahan (data diskrit) adalah data yang diperoleh

         dengan cara membilang. Misalnya, data tentang

         banyak anak dalam keluarga.

     b) Data ukuran (data kontinu) adalah data yang diperoleh

         dengan cara mengukur. Misalnya, data tentang

         ukuran tinggi badan murid.

2)  Data kualitatif adalah data yang bukan berbentuk bilangan.

     Data kualitatif berupa ciri, sifat, atau gambaran dari kualitas

     objek. Sebagai contoh, data mengenai kualitas pelayanan, 

     yaitu baik, sedang, dan kurang.

Cara untuk mengumpulkan data, antara lain adalah melakukan

wawancara, mengisi lembar pertanyaan (questionery), melakukan pengamatan (observasi), atau menggunakan data yang sudah ada, misalnya rataan hitung nilai rapor.

Menyajikan Data dalam Bentuk Diagram

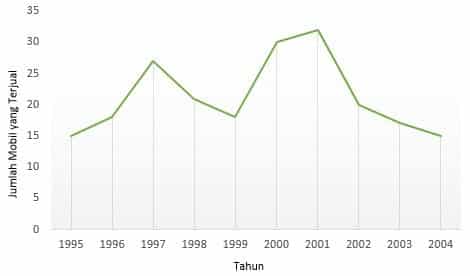
1. Diagram Garis

Contoh:

Pada akhir 1995 – 2004, dealer mobil selalu mencatat jumlah mobil yang dijual, berikut adalah laporannya :

Maka, pembuatan diagram garis pada contoh soal di atas adalah :

2. Diagram Batang

Contoh!

Dari tabel tersebut kita dapat menggambar diagram batang yang menyajikan suhu terendah dan tertinggi dari masing-masing kota sekaligus. Perhatikan diagram batang berikut!

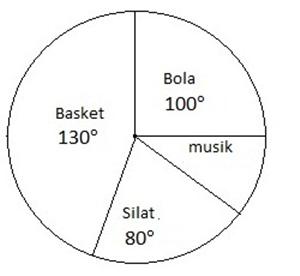
3. Diagram Lingkaran

Contoh 
Sebuah sekolah memiliki 1260 siswa. Di sekolah tersebut mengharuskan siswanya untuk ikut serta dalam kegiatan eskul. Jika siswa yang mengikuti eskul dibentuk dalam diagram lingkaran dalam bentuk derajat (°) sebagai berikut :

 

MEDIAN

1) Median untuk data tunggal

    Median adalah suatu nilai tengah yang telah diurutkan. Median dilambangkan Me.

    Untuk menentukan nilai  Median  data tunggal dapat dilakukan dengan cara:

    a) mengurutkan data kemudian dicari nilai tengah,

    b) jika banyaknya data besar, setelah data diurutkan, digunakan rumus:

      Untuk n ganjil  : Me = X1/2(n + 1)

                                           Xn/2  + Xn/2 +1

      Untuk n genap: Me =   ––––––––––––

                                                   2

      Keterangan:

      xn/2 = data pada urutan ke-n/2 setelah diurutkan. 

      Contoh:

      Tentukan median dari data: 2, 5, 4, 5, 6, 7, 5, 9, 8, 4, 6, 7, 8

      Jawab:

      Data diurutkan menjadi: 2, 4, 4, 5, 5, 5, 6, 6, 7, 7, 8, 8, 9

      Median = data ke-(13 + 1)/2 = data ke-7

      Jadi mediannya = 6

 MODUS DATA TUNGGAL

Modus ialah nilai yang paling sering muncul atau nilai yang mempunyai frekuensi tertinggi. 

1) Modus data tunggal    Modus dari data tunggal adalah data yang sering muncul atau data dengan    frekuensi tertinggi.    Perhatikan contoh soal berikut ini.    Contoh:    Tentukan modus dari data di bawah ini.    2, 1, 4, 1, 1, 5, 7, 8, 9, 5, 5, 10    Jawab:    Data yang sering muncul adalah 1 dan 5. Jadi modusnya adalah 1 dan 5.

Kuartil (Q)

Seperti yang sudah dibahas sebelumnya, bahwa median membagi data yang telah diurutkan menjadi dua bagian yang sama banyak. Adapun kuartil adalah membagi data yang telah diurutkan menjadi empat bagian yang sama banyak.1) Kuartil data tunggal    Urutkan data dari yang kecil ke yang besar, kemudian tentukan kuartil dengan rumus sebagai berikut:

Contoh:

    Tentukan Q1, Q2, dan Q3 dari data : 3, 4, 7, 8, 7, 4, 8, 4, 6, 9, 10, 8, 3, 7, 12.

     Jawab:

     Langkah 1: urutkan data dari  kecil ke besar sehingga diperoleh 

                      3, 3, 4, 4, 4, 6, 7, 7, 7, 8, 8, 8, 9, 10, 12.

                                                 1(15+1)

     Langkah 2: Letak data Q1=–––––––– = 4

                                                      4

                      Jadi Q1 terletak pada data ke-empat yaitu 4

                                                 2(15+1)     Langkah 3: Letak data Q2=–––––––– = 8                                                      4                      Jadi Q2 terletak pada data ke-delapan yaitu 7

                                                 3(15+1)     Langkah 4: Letak data Q1=–––––––– = 12                                                      4                      Jadi Q3 terletak pada data ke-duabelas yaitu 8

 Rumus – Rumus dari Statiska Matematika

• Mode Rumus untuk Data Individual
  Untuk mencari mode dari data individual, cukup cari beberapa nilai.
  Sebagai contoh, ada data individu sebagai berikut: 2,3,5,7,3,4,7,8,4,6,4,5,4
  Dari data individu di atas adalah mode 4 (off 4 kali)

Rumus Rata Tunggal

CONTOH 1

Hitunglah rata-rata dari data $6, 6, 4, 6, 2, 5, 5, 6, 7, 6, 8$!

Jawab:

Dari data tersebut dapat kita ketahui bahwa jumlah data adalah 11 $(n = 11)$. Dengan menggunakan rumus kita dapat menghitung rata-ratanya.$\begin{aligned} \bar{x} &= \frac{1}{n}\sum_{i=1}^{n}x_i \\ &= \frac{1}{11}\left (6+6+4+6+2+5+5+6+7+6+8\right ) \\ &= \frac{1}{11}(61) \\ &\approx 5\text{,}55 \end{aligned}$

Rata-rata dari data tersebut adalah $5\text{,}55$.

CONTOH 2

Berikut ini adalah data nilai mahasiswa untuk mata kuliah statistika, nilai mahasiswa diurutkan dari yang terendah ke yang tertinggi:$4, 4, 4, 5, 5, 5, 5, 5, 6, 6, 6, 6, 7, 7, 7, 7, 7, 7, 8, 9$Menurut pertimbangan dosen, mahasiswa harus mengulang ujian kembali untuk memperbaiki nilai apabila nilai yang mereka dapatkan berada di bawah rata-rata. Berapa orangkah yang harus memperbaiki nilainya tersebut?

Jawab:

Sebelum menghitung jumlah mahasiswa yang harus memperbaiki nilainya, kita harus menghitung dulu rata-rata nilai tersebut. Diketahui banyaknya data adalah 20 $(n = 20)$, sehingga nilai rata-ratanya dapat dihitung sebagai berikut.$\begin{aligned} \bar{x} &= \frac{1}{n}\sum_{i=1}^{n}x_i \\ &= \frac{1}{20}\left (4+4+ \cdots +9\right ) \\ &= \frac{1}{20} (120) \\ &= 6 \end{aligned}$Rata-rata nilai mahasiswa adalah 6, dengan demikian mahasiswa yang harus mengulang ujian adalah mahasiswa yang nilainya berada di bawah 6. Jumlah mahasiswa yang nilainya di bawah 6 adalah 8 orang.

untuk lebih paham lagi, liat vidio menentukan rata - rata berikut 

KLIK KELAS XI IPA UNTUK MENGERJAKAN SOAL

Share this post